一、确定样本量时考虑的因素
结合抽样理论以及收听率调查的实际情况,在确定样本量时,主要需考虑以下因素:
1. 调查总体中的各个体的差异程度。调查总体中各个体的差异程度越大,为了保证达到一定的抽样精度,所需要调查的样本量也应该越大;反之,个体差异程度越小,为达到一定的抽样精度所需要调查的样本量就越小。
2. 抽样方法。 “在概率抽样中,用样本统计量估计总体参数的方法以及这种估计的精度都与具体的抽样方法有关”[1]。抽样方法不同,其调查效率也不同,即使用不同的抽样方法,若要达到相同的抽样精度,所需要的样本量往往不同。
3. 允许误差。在抽样调查中的允许误差越小,即以样本标志值对总体标准值进行推断时的精确度越高,则所需调查的样本量就应该越大;反之,允许误差越大,则所需的样本量就越少。
4. 调查对决策的重要性及调查经费。一般说来,在抽样调查中所需要投入的经费会随着样本量的增加而增加。因而,针对某一项抽样调查所需要的费用就成为确定样本量时必须考虑的一个重要因素。
5. 调查时间要求及人力资源限制。同样,在抽样调查中的样本量越大,完成调查所需要时间和人力就越多。即使在委托专业调查公司实施而不需要考虑人力资源问题的情况下,对获得调查结果的时间缓急程度也往往是确定样本量时需考虑的因素。
6. 成功率(或拒访率、回收率)。在抽样调查中,调查的成功率也是在确定调查样本量时必须考虑的因素,因为成功访问(或回收)的合格问卷或日记卡,才能够被用作进一步的数据统计和分析。
在实际运作中,对于某一特定总体进行抽样调查样本量设计时,调查总体、抽样方法往往已经确定,调查时间、人力资源和成功率等因素因为委托调查公司操作可不予考虑。在这样的情况下,通常确定样本量只需考虑允许误差和调查经费两个因素,而这两个因素之间是一种此消彼涨的关系。即允许误差越小,所需调查的样本量越大,调查费用也就越高;反之,允许误差越大,所需调查的样本量越少,调查费用也就越低。因此,调查样本量的大小实际上是允许的抽样误差(精确度)与调查费用之间相互平衡的结果。
二、收听率调查中样本量的确定
根据抽样理论,在简单随机抽样的情况下,计算样本量时需考虑三个要素:
1. 置信度。根据正态分布的特性,通常采用的置信水平(即占标准正态分布曲线下方的总面积的比例)与相应的标准正态分布的双侧分位数(也称概率度)如表2.2.1:
表2.2.1 部分置信度水平及其在标准正态分布下的对应值
|
置信度
|
50%
|
68.4%
|
75%
|
80%
|
85%
|
90%
|
95%
|
99%
|
99.9%
|
|
概率度
|
0.677
|
1
|
1.146
|
1.281
|
1.441
|
1.646
|
1.961
|
2.576
|
2.81
|
2. 误差度D。它反映的是基于样本的估计值与母体的实际值(总体值)之间的绝对差异水平(绝对误差),一般根据调研者对允许误差的大小需求来确定。
3. 倾向度P。它反映所抽取样本倾向某种情况的可能性,在收听率调查中即代表广播接触率。在倾向度P难以估计时,通常取P(1–P)的数学最大值0.25,这是因为此时P(1–P)在所有可能的广播接触率水平下达到最大。
在简单随机抽样的情况下,样本量的计算公式如下:
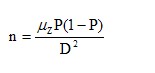 (式2.2.1) (式2.2.1)
其中:n为样本量,P为广播接触率,为概率度,D为允许误差。
根据上述公式,在一定的置信度下,当取数学最大值时,样本量n的多少就取决于允许误差D的大小。表2.2.2和图2.2.1反映了样本量n与允许误差D之间的变动关系。
表2.2.2 不同允许误差水平所需的最少样本量
|
允许误差范围
|
在90%置信度下
|
在95%置信度下
|
在99%置信度下
|
|
±0.01
|
6773
|
9614
|
16589
|
|
±0.02
|
1693
|
2403
|
4147
|
|
±0.03
|
753
|
1068
|
1843
|
|
±0.04
|
423
|
601
|
1037
|
|
±0.05
|
271
|
385
|
664
|
|
±0.06
|
188
|
267
|
461
|
|
±0.07
|
138
|
196
|
339
|
|
±0.08
|
106
|
150
|
259
|
|
±0.09
|
84
|
119
|
205
|
|
±0.1
|
68
|
96
|
166
|
图2.2.1 在95%置信度下样本量与允许误差水平的关系
由表2.2.2和图2.2.1可以看出,随着允许误差的降低,所需要的样本量就越大,但是样本量的增加与允许误差的降低二者之间的关系并不是简单的线性关系。当允许误差较大时,随着允许误差的减小,所需的样本量增加,但增加幅度不大;当允许误差较小时,随着允许误差的减小,所需的样本量则大幅增加。例如,在95%的置信度下,收听率调查的允许误差由±0.04降到±0.03,所需的最小样本量由601个增加到1068个;若允许误差由±0.03降到±0.02,所需的最小样本量由1068个增加到2403个,增加了一倍多;若允许误差由±0.02降到±0.01,所需的最小样本量由2403个增加到9614个,增加了三倍。上述样本量与允许误差的变动关系说明,当允许误差降低到一定程度时,再降低允许误差,所需要的样本量成倍增加,样本量成倍增加意味着调查费用的大幅增加。换言之,样本量和调研费用的大幅增加所能够带来的抽样误差的减小非常有限,这时再增加样本量是不经济的。
需要说明的是,根据抽样理论,当总体N足够大时,样本量n的大小与调查总体并没有直接的关系,所以在确定样本量时一般不需要考虑总体单位数量的大小问题。在收听率调查中,人口多的大城市和人口较少的中小城市所需的最小样本量在理论上是一样的。
因此,综合权衡抽样误差和调研费用的关系,在收听率调查中,一个地区比较合理的样本规模是1068个样本,按照目前家庭户均人口3.5人计算,为300户左右。所以,调查公司通常建议客户在一个城市进行收听率调查的有效样本量为300户。对于一些电台/频率众多、竞争激烈的特大城市,在调查费用允许的前提下,可考虑抽取500户甚至更多样本;而对于一些中小城市,基于节约调查费用的考虑,可选择200户调查样本。
(转载自《广播收听率调查方法与应用》,黄学平主编,中国传媒大学出版社出版)
[1] 《抽样调查理论与方法》P21,冯士雍、倪加勋、邹国华编著,中国统计出版社
|
